Example: Interpreting The Confusion Matrix
This example of an Confusion Matrix is based on one specific threshold and associated with a specific percentage of the population and a specific percentage of attained positive target.
Example
A company wants to do a marketing campaign. They would like to target the campaign to
the customers that will answer positively to the campaign and to avoid unecessary costs.
They have built a model to classify the customers into two categories:- Positive Targets (Predicted 1 and Actual 1): The customers will response positively to the campaign and need to be contacted.
- Negative Targets (Predicted 0 and Actual 0): The customers will response negatively to the campaign and don't need to be contacted.
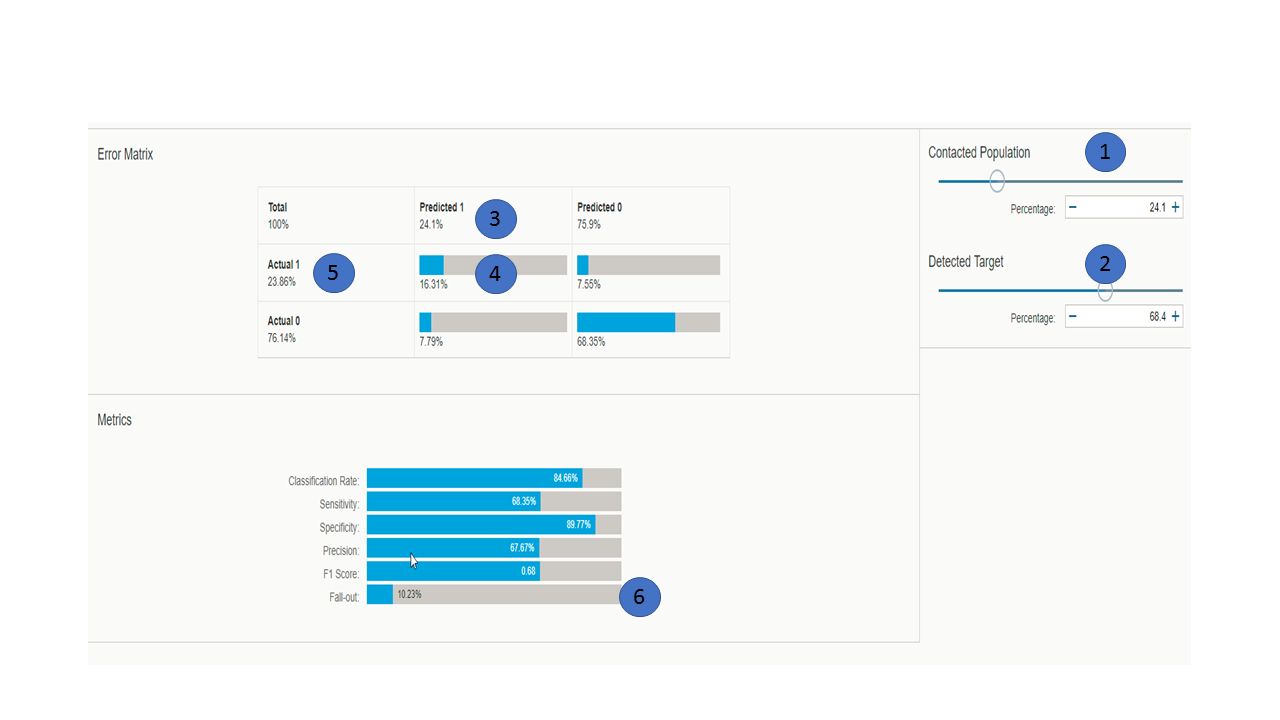
As a result the Confusion Matrix looks the following:
How to read the
results?
- By default, the application proposes to contact 24.1% of the population (see
1 on the graphic below). NoteThe population is sorted in decreasing score order.
- With this threshold:
- You reach 68.4% of the actual positive cases (see 2).NoteAbove this threshold, customers will not be targeted for marketing actions.
- 24.1% of the population (see 3) is considered as positive cases and is selected in the marketing campaign.
- The percentage of "True Positives" is 16.31% (see 4) whereas the percentage of actual positives is 23.86% (see 5).
- You reach 68.4% of the actual positive cases (see 2).
What about the metrics? (see 6)
- The Classification rate is 84.6%. This means that almost 85% of the customers will be correctly classified in the two categories (answer positively/answer negatively to the campaign) when you will apply the validation data source.
- The sensitivity is 68.35%. This means that almost 70% of customers that will answer positively to the campaign are correctly predicted as positive targets. These customers will be selected for the campaign.
- The Specificity is 89.77%. This means that almost 90% of customers that will answer negatively to the campaign are correctly predicted as negative targets. These customers will not be contacted for the campaign.
- The Precision is 67.67%. This means that almost 70% of customers predicted as customers that will answer positively to the campaign are correctly classified. These customers will be part of the campaign.
- The F1 Score is 0.68%.
- The Fall-out is 10.23%. This means that almost 10% of the customers that will answer negatively to the campaign are classified as positive targets and will be selected for the marketing campaign.